Решаем уравнения путем подбора параметра в Excel
Задача решения уравнения встает не только перед студентами и школьниками. В Excel можно использовать различные способы выполнения этой задачи. О способе решения путем подбора параметра пойдет речь в этой статье.
Нахождение корней нелинейного уравнения с использованием средства «Подбор параметра» сводится в двум этапам:
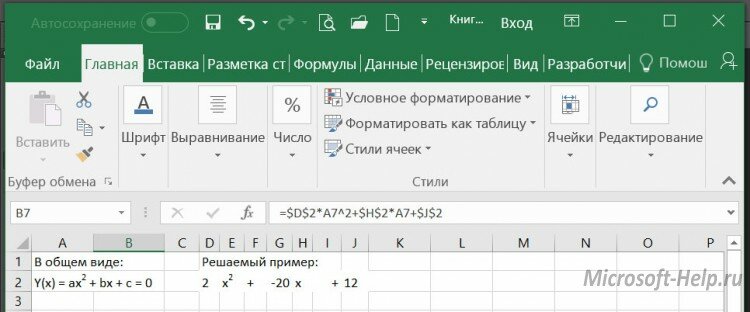 Чтобы оценить примерные границы отрезков и количество корней, можно использовать табличное задание значений функции, т.е. задать несколько значений переменной и вычислить соответствующие значения функции. Опять же, для того, чтобы можно было моделировать расчеты для квадратных уравнений с различными коэффициентами, шаг табулирования лучше задать в отдельной ячейке. Начальное значение переменной можно будет изменять путем ввода в ячейку «А6». Для вычисления следующего значения в ячейку «А7» введена формула «=А6+$B$4», т.е. использована абсолютная ссылка на ячейку с шагом табулирования.
Чтобы оценить примерные границы отрезков и количество корней, можно использовать табличное задание значений функции, т.е. задать несколько значений переменной и вычислить соответствующие значения функции. Опять же, для того, чтобы можно было моделировать расчеты для квадратных уравнений с различными коэффициентами, шаг табулирования лучше задать в отдельной ячейке. Начальное значение переменной можно будет изменять путем ввода в ячейку «А6». Для вычисления следующего значения в ячейку «А7» введена формула «=А6+$B$4», т.е. использована абсолютная ссылка на ячейку с шагом табулирования.
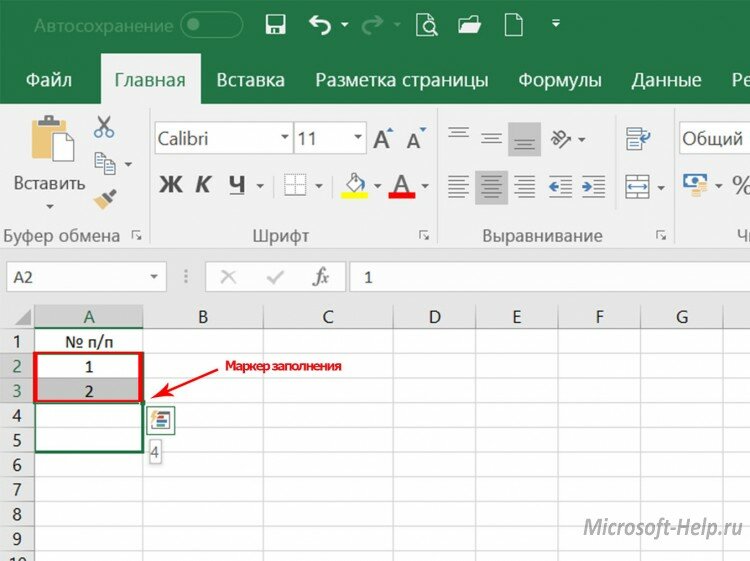
 Далее с помощью маркера заполнения формируется ряд формул для вычисления последующих значений переменной, в приведенном примере используется 20 значений.
Далее с помощью маркера заполнения формируется ряд формул для вычисления последующих значений переменной, в приведенном примере используется 20 значений.
Вводится формула для вычисления значения функции (для рассматриваемого примера в ячейку «В6») и формируется ряд аналогичных формул для остальных ячеек. В формуле использованы абсолютные ссылки на ячейки с коэффициентами уравнения.
 По построенной таблице строится точечная диаграмма.
По построенной таблице строится точечная диаграмма.
 Если начальное значение Х и шаг выбраны неудачно, и на диаграмме нет пересечений с осью абсцисс, то можно ввести другие значения и добиться нужного результата.
Если начальное значение Х и шаг выбраны неудачно, и на диаграмме нет пересечений с осью абсцисс, то можно ввести другие значения и добиться нужного результата.
Можно было бы найти решение уже на этом шаге, но для этого понадобилось бы гораздо больше ячеек и шаг, равный заданной точности вычислений (0,001). Чтобы не создавать громоздких таблиц, далее используется «Подбор параметра» из группы «Прогноз» на вкладке «Данные». Предварительно необходимо выделить место под начальные значения переменной (корней в примере два) и соответствующие значения функции. В качестве «х1» выбирается первое из значений, дающих наиболее близкое к нулю значение функции (в примере 0,5). В ячейку L6 введена формула для вычисления функции. В окне подбора параметра необходимо указать для какой ячейки (L6), какое значение (0) нужно получить, и в какой ячейке для этого изменять значения (К6).
 Для поиска второго корня необходимо ввести второе из значений, дающих наиболее близкое к нулю значение функции (в примере 9,5), и повторить подбор параметра для ячейки L9 (в ячейку скопирована формула из ячейки L6).
Для поиска второго корня необходимо ввести второе из значений, дающих наиболее близкое к нулю значение функции (в примере 9,5), и повторить подбор параметра для ячейки L9 (в ячейку скопирована формула из ячейки L6).
 Предложенное оформление коэффициентов функции в отдельные ячейки позволяет без изменения формул решать другие подобные уравнения.
Предложенное оформление коэффициентов функции в отдельные ячейки позволяет без изменения формул решать другие подобные уравнения.
 Подбор параметра имеется и в более ранних версиях программы.
Подбор параметра имеется и в более ранних версиях программы.
Нахождение корней нелинейного уравнения с использованием средства «Подбор параметра» сводится в двум этапам:
- определение приблизительных границ отрезков и количества корней графическим методом;
- подбор на каждом отрезке значения корня, удовлетворяющего заданной точности вычислений.
 Чтобы оценить примерные границы отрезков и количество корней, можно использовать табличное задание значений функции, т.е. задать несколько значений переменной и вычислить соответствующие значения функции. Опять же, для того, чтобы можно было моделировать расчеты для квадратных уравнений с различными коэффициентами, шаг табулирования лучше задать в отдельной ячейке. Начальное значение переменной можно будет изменять путем ввода в ячейку «А6». Для вычисления следующего значения в ячейку «А7» введена формула «=А6+$B$4», т.е. использована абсолютная ссылка на ячейку с шагом табулирования.
Чтобы оценить примерные границы отрезков и количество корней, можно использовать табличное задание значений функции, т.е. задать несколько значений переменной и вычислить соответствующие значения функции. Опять же, для того, чтобы можно было моделировать расчеты для квадратных уравнений с различными коэффициентами, шаг табулирования лучше задать в отдельной ячейке. Начальное значение переменной можно будет изменять путем ввода в ячейку «А6». Для вычисления следующего значения в ячейку «А7» введена формула «=А6+$B$4», т.е. использована абсолютная ссылка на ячейку с шагом табулирования. Далее с помощью маркера заполнения формируется ряд формул для вычисления последующих значений переменной, в приведенном примере используется 20 значений.
Далее с помощью маркера заполнения формируется ряд формул для вычисления последующих значений переменной, в приведенном примере используется 20 значений.Вводится формула для вычисления значения функции (для рассматриваемого примера в ячейку «В6») и формируется ряд аналогичных формул для остальных ячеек. В формуле использованы абсолютные ссылки на ячейки с коэффициентами уравнения.
 По построенной таблице строится точечная диаграмма.
По построенной таблице строится точечная диаграмма. Если начальное значение Х и шаг выбраны неудачно, и на диаграмме нет пересечений с осью абсцисс, то можно ввести другие значения и добиться нужного результата.
Если начальное значение Х и шаг выбраны неудачно, и на диаграмме нет пересечений с осью абсцисс, то можно ввести другие значения и добиться нужного результата.Можно было бы найти решение уже на этом шаге, но для этого понадобилось бы гораздо больше ячеек и шаг, равный заданной точности вычислений (0,001). Чтобы не создавать громоздких таблиц, далее используется «Подбор параметра» из группы «Прогноз» на вкладке «Данные». Предварительно необходимо выделить место под начальные значения переменной (корней в примере два) и соответствующие значения функции. В качестве «х1» выбирается первое из значений, дающих наиболее близкое к нулю значение функции (в примере 0,5). В ячейку L6 введена формула для вычисления функции. В окне подбора параметра необходимо указать для какой ячейки (L6), какое значение (0) нужно получить, и в какой ячейке для этого изменять значения (К6).
 Для поиска второго корня необходимо ввести второе из значений, дающих наиболее близкое к нулю значение функции (в примере 9,5), и повторить подбор параметра для ячейки L9 (в ячейку скопирована формула из ячейки L6).
Для поиска второго корня необходимо ввести второе из значений, дающих наиболее близкое к нулю значение функции (в примере 9,5), и повторить подбор параметра для ячейки L9 (в ячейку скопирована формула из ячейки L6). Предложенное оформление коэффициентов функции в отдельные ячейки позволяет без изменения формул решать другие подобные уравнения.
Предложенное оформление коэффициентов функции в отдельные ячейки позволяет без изменения формул решать другие подобные уравнения. Подбор параметра имеется и в более ранних версиях программы.
Подбор параметра имеется и в более ранних версиях программы.
microsoft
5-10-2017
Комментариев: 0

 Создаем последовательности данных в Excel
Создаем последовательности данных в Excel Округляем числа в Excel
Округляем числа в Excel Создаем «напоминалку» в Excel
Создаем «напоминалку» в Excel Переносим таблицу из Excel в Word
Переносим таблицу из Excel в Word Как создать (вставить) формулу в Excel
Как создать (вставить) формулу в Excel Подсчитываем количество ячеек в Excel
Подсчитываем количество ячеек в Excel